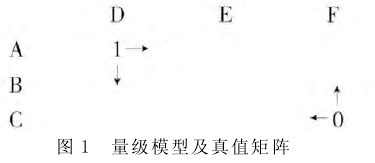
 这些“量级命题”(scalar propositions)构成一个真值矩阵,彼此之间具有衍推关系:同一道题,如果小学生能做,那么中学生和大学生也能做;中学生能做,那么大学生也能做。同一个教育程度,做不了简单题,那么也做不了中等题和复杂题,做不了中等题,那么也做不了复杂题。图1中左上角的1表示,最容易成立的肯定命题是 AD(大学生能做简单题);右下角的0表示,最容易成立的否定命题是CF(小学生做不了复杂题)。其中1和0的箭头指向表明,如果知道矩阵中某一命题为真,那么其上方和左方的命题也为真;而如果知道矩阵中某一命题为假,那么其下方和右方的命题也为假。换言之,从0到1表示命题成立可能性由高到低,而从1到0代表命题成立可能性由低到高。〔11〕(相关分析参见沈家煊2001)上面对三种句式量级关系的讨论,都可以建立在量级命题是否为真的基础之上,同时句内命题同语境命题的关系也得到了很好的体现。 特别需要强调的是,时间量级在衍推机制上有其独特之处。当焦点项的命题实现时,往往不能推出其较早的命题同时成立或实现,而是推出较早的命题曾经成立或实现。这是因为广义的时间量级实际上是由两个平行维度的事件量级和时间量级共同组成的复合语用量级。如当命题“他(今年)三十岁了”成立时其“年龄变化”事件量级为{……二十九岁,三十岁,三十一岁,……},其参照时间量级为{……去年,今年,明年,……}。这个复合量级严格遵守语用量级的衍推规则,其衍推命题为“他(去年)二十九岁”同时成立。由于句尾“了”同句内命题的参照时间“今年”相关,那么从“今年”这一参照点看“去年”相关联的命题,其获得的衍推命题就是“他曾经是二十九岁”。因此句尾“了”关联的“事件-时间”量级在不强调参照时间的情况下,其衍推意义往往表示较早命题曾经实现。 综上所述,句尾“了”在量级模型中同焦点项所在的实现命题相关联,其左侧和上方的命题过去成立或曾经实现,用-1表示,而其右侧和下方的命题不成立或尚未实现,用0表示。因此句尾“了”所在的实现命题可以将量级模型区分为“曾经发生”矩阵和“尚未发生”矩阵两个部分。 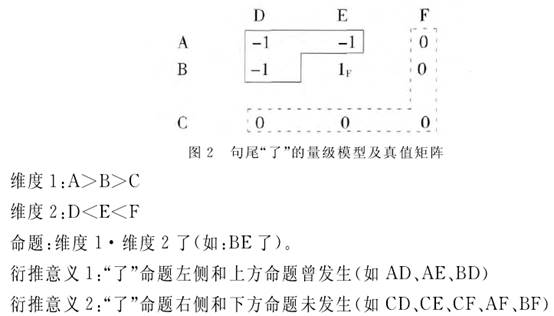 如图2所示,在所举的例子中,两个维度之间的关系是句内命题和语境命题的关系。在更为复杂的句式中,第二个维度即语境命题可能成为句内成分,同句内命题互相参照,共同构成整体的复杂命题,这就涉及到语用量级的倒置规则及理据,下一节将展开分析。 (责任编辑:admin) |
