|
由f’(p)=0得,p=1/2。进一步由f’’(1/2)=8>0,知p=1/2是极小值点,对应的极小值为f(1/2)=4(1/2)2-4.5+1=0。而f(0)=f(1)=1,说明该点为最小值点。函数的最小值为零,说明函数为非负函数,因此这个策略可以满足在非负意义下的最优。采用这样的方法,不一定使期望收益最大化,可以理解为是期望损失最小。它以一定的概率在两种意思间变化,在重复执行时会得到不同的结果,能够修正错误。我们将这种方法称为基本博弈论方法。 在传统的方法中,上下文信息是进行歧义消解的重要根据。在博弈论模型的求解过程中同样也可以充分利用上下文的信息。博弈论的研究结果表明,解决这类无支付占优与风险占优区分的协调博弈的唯一方法是沟通。在歧义消解的过程中就是信息的发送者和接收者之间的沟通。实际上在任何语境当中,信息的发送者或多或少的给接收者发出了一定的信息,我们称为上下文信息,在博弈论中称为边信息。如果在上下文的信息中有“一份”存在,它是表示个体的量词短语,因此可以判断“牛奶咖啡”表示定中关系,是一种食物,有牛奶的咖啡;如果在上下文的信息中有“都”存在,它是表示将两种东西共存的副词,因此“牛奶咖啡”表示并列关系,是两种食物:牛奶和咖啡。如果接收者能够准确地捕捉和理解这些信息,则博弈双方就实现了沟通和协调,从而博弈可以稳定在某个均衡点上。 发送者在每次传递信息过程中对特定的类型发送特定的信息,与接收者进行沟通,接收者可以通过对这些意思的判断来选择自己的策略,达到消除歧义的目的。例如假定发送者会发送两种类型的信息x1或x2;两种类型的伴随信息m1或m2,那么接收者在收到信息m1时,判断发送者发送的类型为x1的后验概率是: 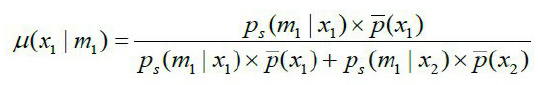 其中概率ps(m|x)表示类型x的发送者发送信息m的概率。例如当“m1=一份”时,ps=0.7,那么在这种情况下的后验概率μ(x1|m1)=90.32%,此时信息接收者选择x1,达到均衡的概率就增加到了90.32%,这比单纯通过统计的方法要准确得多。同样我们可以计算出μ(x1|m2),μ(x2|m1)和μ(x2|m2)接收者可以根据不同的接收信息来计算后验概率,然后和先验概率进行比较,从而得出最优的行动。利用博弈论的理论和方法,我们在歧义消除过程中,尤其是在机器翻译过程中就有了具体的理论支持和可靠的操作方法,同时还有了明确度量方法好坏的标准。我们将这种方法称为包含上下文信息的博弈论方法。上述博弈论模型是根据图1所示的收益矩阵建立的,在实际应用过程中,对于一个歧义问题,它被成功消除产生的收益和歧义产生的惩罚不一定对等。它的消解结果对发送者和接收者产生的影响也不一定相等,此时收益矩阵不再是如图1所示的对等的矩阵,而是一个非对等博弈矩阵模型。如图2所示。 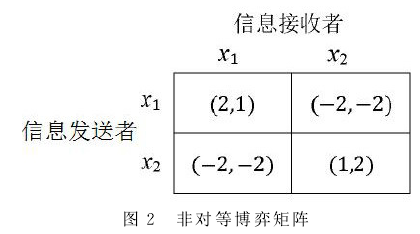 在这个博弈矩阵下,消歧的结果对双方的收益是不同的,显然也不存在纯纳什均衡,该模型仅存在混合策略的纳什均衡。接收者再根据(1)式计算自己的策略时,则得到的结果也会产生变化。显然当歧义的意思有两种以上的选择时,博弈的矩阵形式和求解的具体过程也会有相应的变化。 上面我们给出了三种消解结构歧义方法,第一种方法是根据每种意思出现的概率的大小,直接选择出现概率大的意思作为问题的解。第二种方法根据博弈论的混合策略原理进行选择。第三种方法使用上下文信息选择博弈模型的混合策略。 (责任编辑:admin) |
