数学科普的华彩篇章
http://www.newdu.com 2025/12/07 10:12:23 中华读书报 刘懿 参加讨论
原标题:《华罗庚科普著作选集》:数学科普的华彩篇章 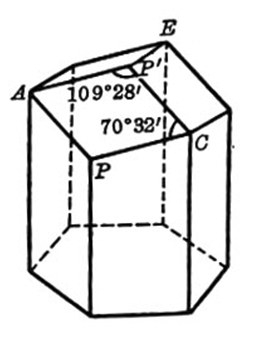 图1 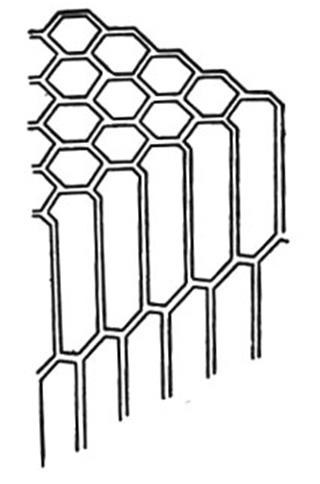 图2  《大哉数学之为用——华罗庚科普著作选集》,华罗庚著,上海教育出版社2018年12月第一版,88.00元 华罗庚是中国解析数论、典型群、矩阵几何学、自守函数论与多个复变函数论等很多方面研究的创始人与开拓者,也是中国计算机研究事业的开创者和奠基人,是我国进入世界著名数学家行列最杰出的代表。华罗庚是中国科学院院士、美国国家科学院外籍院士、德国巴伐利亚科学院外籍院士。美国数学家Batman曾说过,华罗庚是中国的爱因斯坦,足够成为全世界所有著名科学院的院士。 华罗庚的一生充满传奇色彩。他自小家境贫寒,初中毕业就辍学了,通过自学掌握了高中数学和大学微积分知识。20岁时,华罗庚被熊庆来发现而破格进入清华大学,由图书管理员做起,后转为助教。因聪明才智和突出表现,得到著名数学家维纳和阿达玛的赏识,被推荐到剑桥大学,师从哈代等数学大师。在剑桥,华罗庚没有选择读博士学位,而是抓紧时间选择多学知识和多做研究工作,被誉为“剑桥的光荣”。1938年华罗庚回国受聘于西南联大,在抗日战争的炮火声中从事教学与研究,从助理员到教授前后只用了7年时间。1946年华罗庚受邀分别赴苏联和美国普林斯顿高等研究院访问,并被伊利诺伊大学聘为教授。中华人民共和国成立后,华罗庚放弃了在美国的优裕生活,于1950年毅然回国。在这之后的三十多年里,他从思考中国数学的发展战略,绘制发展蓝图,到学科规划与布局,从召唤国外留学人才回国参加建设,到积极培养青年学生,倾注了满腔热忱。为了使数学能够更好地为国家经济建设服务,为了促进中国应用数学的发展,他从纯粹数学的理论研究转到应用数学的研究领域,一干就是20余年。1985年6月12日,华罗庚在东京大学作完一场学术报告后,因心脏病发作倒在讲台上,为自己的传奇人生画上了一个句号和惊叹号。 华罗庚不仅是应用数学理论的研究者,也是数学文化的传播者。他在生命的后半程里,走出书斋,到学校、到工农业生产一线,走了祖国27个省市,倾情进行科学传播与普及工作。他写了大量的数学科普文章,从对传统数学问题的发掘演绎,到把抽象高深的数学原理作通俗化的创造性解析,再到在生产生活实际中推广数学方法的应用,深入浅出,娓娓道来,引人入胜,使具备中学数学水平的人就能入门学习。这些作品得到了国内外数学界和教育界的高度赞誉。 请看华罗庚谈“蜂房问题”的华彩篇章。 蜜蜂是无与伦比的伟大建筑师,在人类有史以前就用蜂蜡建造出了密合度最高、所需材料最简、可使用空间最大的蜂房,其展现出的数学才华,令人类啧啧称奇。艺术家们模仿蜂巢做出了各种艺术品,工程师们利用蜂巢原理来改善房屋的建筑性能,科学家通过对蜂房的研究,把蜂房的原理应用到了通信、飞机和航天器等领域……数学家华罗庚是怎么看待蜂房问题的呢? 1.始于“有趣” 华罗庚是在一本通俗读物中看到有关蜂房的内容描述的,18世纪初,法国学者马拉尔琪曾经测量过蜂窝的尺寸,得到一个有趣的发现,六角形窝洞的六个角都有一个一致的规律:钝角等于109°28',锐角等于70°32'。法国物理学家列奥缪拉由此得到一个启示,蜂窝的形状是不是为了使材料最节约而容积最大呢?瑞士数学家克尼格也得出了类似的结论:要消耗最少的材料制成最大的菱形容器,它的钝角和锐角的角度接近于上述的数值。华罗庚为此深深着迷:小小蜜蜂在人类有史以前所已经解决的问题,竟要18世纪的数学家和物理学家用高等数学才能解决呢! 2.继之“困惑” 什么样的六角形窝洞的钝角等于109°28',锐角等于70°32'?六角形六内角的和等于720°,每个角平均120°,而109°28'与70°32'都小于120°,因而不可能有这样的六角形!“六角形”和“菱形”都是平面图形的术语,怎么用来刻画一个立体结构“窝洞”或“容器”呢? 3.于是“访实” 华罗庚请教了昆虫学家,找个实物蜂房来观察,才知道既说“六角”又说“菱形”的意义。原来从正面来看蜂房是由一些正六边形所组成,每一个角都是120°,并没什么角度的问题。问题在于房底。蜂房并非六棱柱,而是把六棱柱的一端切下三个同样的角,并搬移堆砌,使它的底部由三个相同的菱形所拼接而成(图1)。而蜂巢就是由两排这样的蜂房底部和底部相接而成的(图2)。 4.初步“解题” 初步形成并解决一个数学问题:怎样切出来使所拼成的三个菱形做底的六棱柱的表面积最小? 5.“浅化”“慎微” 尝试寻找最简单的数学工具解决问题,并小心留意,提出的几何问题和解题时所讨论的代数问题不一定是完全等价的。 6.退而“疑古” 经计算而得的容积一样而用材最省的数据比例与实测蜂房的尺寸数据并不相合,因而使人不得不怀疑前人已得的结论。华罗庚为此感叹:往事几百年,祖述前贤,瑕疵讹谬犹盈篇,蜂房秘奥未全揭,待咱向前! 7.切入“正题” 由此看来蜂房问题并不是一个单纯的“体积给定,求用材最小”的数学问题,必须把蜜蜂的“体态”入算,从考虑它的身长、腰围入手,怎样情况用材最省?通过推算,在“量体裁衣”的考量下,形状为尖顶六棱柱的蜂房是最省材料的结构。这生动地说明了生物本身与环境的关系的统一性。至此,蜂房的数学问题算是得到了解决。 8.进而“设问” 华罗庚认为,以上只不过从六棱柱(或四方柱)出发,按一定的切拼方法做了些研究而已。实质上,这样的看法未入事物之本质。为什么仅从六棱柱出发,而不能从三角柱、四方柱或其他柱形出发,乃至于为什么要从柱形出发?更不要说切拼之法也是千变万化了!甚至于为什么要从切拼得来!越想问题越多,思路越宽。比如,由蜂房问题可以引出有名的晶体问题——怎样的体可以作为晶体?也就是说,用同样的体可以无穷无尽地、无空无隙地填满整个空间。由柱体填满空间问题还可想到其等价问题:怎样的样版可以填满平面的问题。进而设想填满一个球或一个圆柱的问题…… 由蜂房启发出来的问题,真是让人浮想联翩,由此及彼,由表及里,回味无穷啊。 华罗庚并未就此止步,为了让进入大学之后的学生还能咀嚼回味思考,他又从“代数”“几何”“推广”“极限”“抽象”等方面对蜂房问题进一步作了深入探讨。 华罗庚之所以把自己的思考过程源源本本地娓娓道来,是想借由对蜂房问题的解析,为我们提供一个思考、解决疑难问题的生动的样例:有趣——困惑——访实——解题——浅化——慎微——疑古——正题——设问——数形结合——推而广之——极限抽象……这样一个思维过程是科学家,特别是数学家,认识问题、解决问题的一般途径。思维方式是探索未知的导航器,习惯于思考联想的人一定会走得深些远些;没有思考联想的人,虽然读破万卷书,依然看不到书外的问题。 以上资料取自华罗庚《谈谈与蜂房结构有关的数学问题》一文。1984年,上海教育出版社出版了《华罗庚科普著作选集》,该书中收录的每一篇文章都得到了华罗庚的过目和认可,上文便是其中的一篇。《选集》出版后获得了无数荣誉,最近的一次是在2018年被评为“改革开放40年中国最具影响力的40本科学科普书”之一。2019年初,上海教育出版社对这部名著作了修订,重新编辑整合梳理,概括提炼内在主旨,书名为《大哉数学之为用——华罗庚科普著作选集》(同时出版的还有华罗庚的弟子王元先生的大作《大哉言数——王元科普著作选集》)。读者可以从书中了解到华罗庚传奇的求学经历,伟大的数学成就,深邃的数学思想和非凡的数学普及工作。 也许有人会问:现在华罗庚的科普作品是否已经过时?答案当然是否定的。就像2000多年前欧几里得的经典几何学,始终是初中数学绕不开的内容,华罗庚当年总结的数学思维规律、数学建模思想,至今都是数学学习的“金钥匙”;华老谈及“杨辉三角”“祖冲之的圆周率”“数学归纳法”“有限与无穷,离散与连续”等内容的篇目,观点高屋建瓴,叙述透彻本原,分析入木三分,如果能读懂读透,则胜过读很多本一般数学普及读物;华老独特的“由薄到厚,再由厚到薄”的读书法,“下棋找高手,弄斧到班门”的求学法,“搜炼古今”的治学法,都是非常高明的。笔者特别赞同本书特约编辑、首都师大数学科学学院方运加先生的观点:没有读过华罗庚经典科普作品的数学教师,不会是最好的数学教师;而认真读了这些作品的学生,一定会是有底气同老师切磋交流的好学生。 近日,中共中央办公厅、国务院印发了《关于进一步弘扬科学家精神加强作风和学风建设的意见》,要求大力弘扬科学家胸怀祖国、服务人民的爱国精神,勇攀高峰、敢为人先的创新精神,追求真理、严谨治学的求实精神,淡泊名利、潜心研究的奉献精神。华罗庚一生的所作所为正是对这种科学家精神的最好诠释。华罗庚先生的学生、中国科学院院士王元先生曾经有言:华老已经离开我们了,他留给我们的精神财富是丰富的,我们要把他的学问、品德与情操告诉后人,使后人从他的事迹中得到启发与教益。在我们看来,《大哉数学之为用——华罗庚科普著作选集》一书并不只是传播数学知识,还承载了上述深刻意义。 (责任编辑:admin) |