自然语言的计算复杂性研究(5)
http://www.newdu.com 2025/12/21 12:12:41 《外语教学与研究》2015年 冯志伟 参加讨论
“我尝到了读书的甜头”,在 Mohawk语中是: 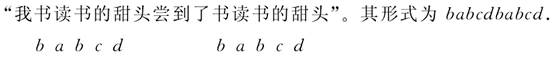 这种结构,与形式语言 L3也很相近,也不能用正则语法生成。 由此可见,正则语法作为一种刻画自然语言的形式模型显得无能为力,这样的语法难以满足自然语言计算复杂性的要求(冯志伟、胡凤国 2011)。 在研究自然语言的计算复杂性的时候,我们首先有必要判定这样的语言是不是正则语言,从而对于这种语言的计算复杂性获得一个初步的认识。 那么,怎样来证明一种语言不是正则语言呢?我们可以采用抽吸引理(pumping lemma)来证明。 让我们来研究一种符号串长度为N的语言L和与它相应的状态图。这个状态图从状态q0开始;在读了一个符号之后,进入状态q1;读了N个符号之后,进入状态qn;长度为N的符号串将通过N+1个状态,就能从状态q0到状态qn。这意味着,在接收的路径上,至少有两个状态必须是相同的(把它们 叫做qi和qj)。因此,在从开始状态q0到最后状态qn的路径上,必定存在回路。 设x是状态图从开始状态q0到回路起点qi读的符号串,y是状态图通过回路时读的符号串,z是从回路终点qj到最后的接收状态qn读的符号串(见图2)。 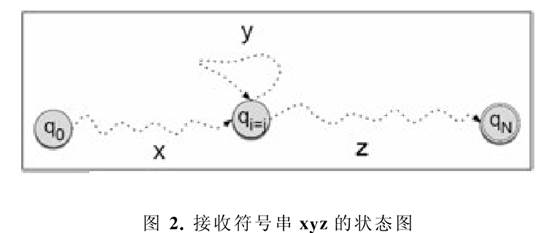 状态图接收由这三个符号x,y,z构成的毗连符号串。但是,如状态图接收了xyz,那么它一定也接收xz。这是因为状态图在处理xz时,可跳过回路,中间的符号y就像被抽水机抽吸了一样。另外,状态图也可在回路上打任意次数的圈儿,这样,它也可接收xyyz,xyyyz,xyyyyz等符号串;在状态图打圈的时候,y一个个被放出来。因此,当n≥0时,状态图可接收形式为 xynz的任何符号串,中间的符号y就像抽水机中的水,一会儿被抽吸进去,一会儿被推放出来。 (责任编辑:admin) |
- 上一篇:计算语言学的理论方法和研究取向
- 下一篇:自然语言处理技术与语言深度计算